数学勉強法(一般論)３～数学が得意な人は１を聞いて１０を知る～

数学の話ばかりですが、構わず続けます。

１回目で数学の勉強であっても、脳に出来るのは(ほぼ)記憶だけだと話しました。

２回目で脳は無意味なことより理解(納得と同義で使っています)した内容の方が覚えやすく、数学が得意な人は、それを利用していると話しました。

今回の内容は、数学が得意な人は理解している点だけが違うのか、という話です。

結論から言うと違います。

今回のキーワードは１を聞いて１０を知るです。

頭がいい人は１つ教えられて１つ覚えるのではなく、１つの教訓から１０の事柄を理解するわけです。

今回も例を出します。

例題１

「１５段の階段がある。１回で１段または２段上ることができる。全部で何通りの上り方があるか。」

これは京大の昔の有名問題です。難しいですね。

場合分けしますか？でもどうやって…？

実は普通の場合の数の問題ではありません。

これは一般化して解きます。

１５段目に行くには１３段目から一気に２段上るか、１４段目から１段上るかの２通りですね。

n段目まで上る方法をa_n通りとすれば、「a₁₃+a₁₄=a₁₅」が成り立ちます。

これは１５段目じゃなくても成り立つので「a_n+a_n+1=a_n+2」が成り立ちますね。

お気づきでしょうか。

フィボナッチ数列になっています。

a₁=1

a₂=2

ですから順に、１、２、３，５、８、１３、２１、３４、５５、８９、１４４、２３３、３７７、６１０、９８７

というわけで１５段の上り方は９８７通りですね。

はい。これは解説を聞けば理解できると思います。

次の例題は、ネタバレになってしまいますが、数Ⅲの内容を使うので、理系でないと厳しいかも知れません。

例題２

「１００^９９と９９^１００の大小を比べろ。」

これもまた有名な問題です。どうでしょうか。

こういう時はlogを取ればいい！と思った方、筋が良いです。

取ってみましょうか。今回は常用対数(底が10)ですね。

log(100⁹⁹)=99×2=198

log(99¹⁰⁰)=(3log3+log11)×100

数Ⅱの問題だったらここで問題文にlog3とlog11の値が載ってるはず…

あれ、載ってない…

というわけで、この問題は数Ⅲなのです。

え、数Ⅲを勉強したけど解けない？

そりゃそうです。難しい(けど良く出来てる)から有名問題なんですから。

実はこれも一般化して解く問題なのです。

｢100⁹⁹と99¹⁰⁰｣の大小と｢99log100と100log99｣の大小は同じですね。今度は自然対数(底がe)にしてみましょう。

さらに、｢log100/100とlog99/99｣の大小も同じですよね。                  

これで一般化出来ます。

つまりlogn/nのグラフを描いてみればいいですね。

このグラフは有名なので微分しないで描けた方が良いですが、一応やります。

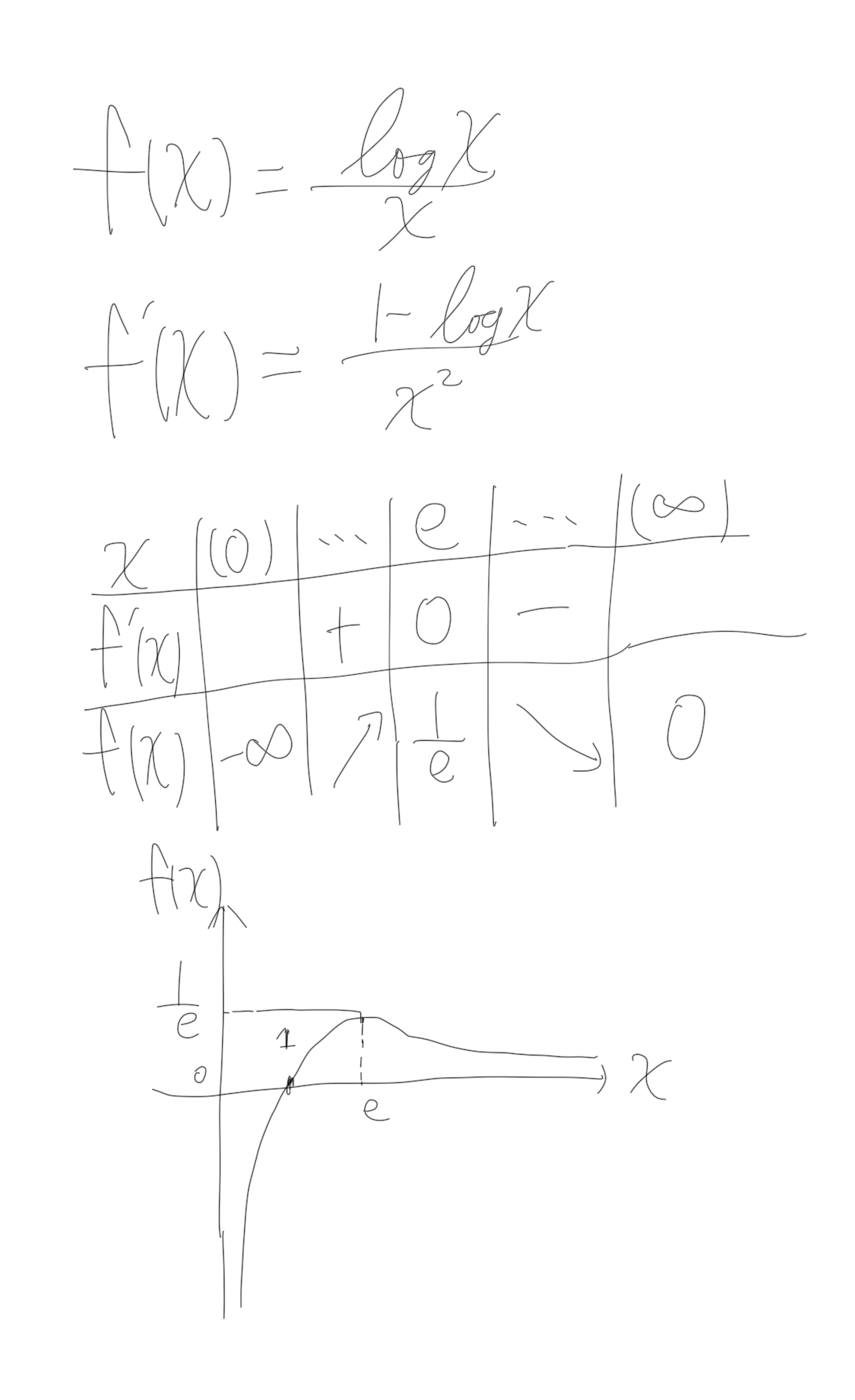
はい。突然画像になりましたが、こんな感じですね。

この図より、nがe(2.7くらい)より大きいときは単調減少なんですね。

だからlog100/100＜log99/99ですね。

よって両辺を9900倍してlogを外せば、100⁹⁹＜99¹⁰⁰ということになります。

いかがでしょう。難しいですね。

この記事で言いたいことはですね。

数学が得意な人は上の例題の片方を聞けばもう片方も解けます。

これが１を聞いて10を知るということです。

一見関係ない２つの問題ですが、実際は｢具体的な数値が与えられているが、そのままやると行き詰まる｣→｢敢えて一般化してみると分かることがある｣

という思考のプロセスが同じなんですね。

これを無意識でやれるのは数学のセンスがある人だけ。

ちなみに生まれて初めて一般化する問題に出会って、試験時間内に解けたら天才です。

それは無理です。数学の才能のある人ですら、普通は、一般化するとできることがあると知った上で思いつくのです。

良い指導者に恵まれたら、上の二つの共通点になるような所を強調してくれるでしょう。

まあ今回は例えのレベルが高かったかも知れませんね。。

良い指導者に巡り会えたら、例題のような問題が出てきたとき、他の問題にも通用する共通点、思考のプロセスを強調してくれるでしょう。

解法から思考のプロセスに変換するというのが具体から抽象への変換と同じですね。