暗記数学と言われる勉強法があります。
これは和田秀樹さんという方が提唱したものです。
彼は日本1の進学校である灘高校を卒業して現役で東大理三に進学した人です。
精神科医をやりながら、たくさん本を書いていて、受験生やその親向けのものも多いのです。
受験方法論の元祖と言える存在です。
彼の方法論は、綺麗事を排除して、合計点で合格すれば良いと言う、
サバサバした現実主義です。
和田秀樹さんの本は絶対に1冊は読んだ方がいいですよ。
私は高校1年の時にブックオフで彼の処女作である「受験は要領」という本をたまたま立ち読みし、目からウロコが落ちました。
その本に出会ってなければ、私は東大理三を目指すこともなく、慶應医学部に入学することもなかったかもしれません。
さて、和田秀樹さんの方法論の目玉の一つに暗記数学というものがあります。
という記事でも書きましたが、私はこのネーミングが絶対に悪いと思いますが、
これについて、曲解されて伝わっていることも多いので、和田秀樹さんがどういう意味で使っていたのか、から解説したいと思います。
Contents
暗記数学とは
暗記数学というのを提唱したのは和田秀樹さんです。
彼曰く、落ちこぼれで数学が苦手だったそうですが、灘高校の人に言われても…というのが普通の反応かも知れません笑
灘高校の中では本当に苦手だったのかも知れませんが、日本人全体で見れば、どんなに低く見積もっても上位数%に入る才能はあったでしょう。
でも、彼が受験生の頃は、数学は、得意な人はできて、不得意な人はできない科目でした。
灘高校という、日本一の進学校でも教育方法が確立していなかったのでしょう。
そして、灘高校には教科書で新しい単元を習ったら、次の瞬間東大の過去問が解けてしまうような”天才”がたくさんいたことでしょう。
だから和田秀樹さんは自分を落ちこぼれと言うのでしょうが…
比べる相手が悪すぎるだけですね。
そして、そういう特別な才能のなかった和田秀樹さんはどうしたかと言うと、
青チャートの例題を丸暗記したんですね。
すると、数学がなまじ得意な人には勝てるようになったと。
（ちなみに灘高校でいうなまじ得意な人というのは、低く見積もっても駿台全国模試で名前がギリギリ載るくらいだと思います。）
そして、彼は確信したんですね。
青チャート例題みたいな基礎〜標準問題を全部覚えたら良いじゃん！と。
これは画期的です。なにせ今まできちんとした方法論がなかったのですから。
そして彼が書いた本で名付けたのが「暗記数学」でした。
暗記数学は正しいのか
これについては、現在でも和田秀樹さんの方法ろんを否定する人はほとんどいません。
私も大いに正しいと思います。
全ての勉強はインプットとアウトプットで出来ています。
数学の勉強が和田秀樹さん以前はアウトプット偏重だったんですね。
それが、和田秀樹さんのおかげで、数学もインプットが大事だと、世に広まったのです。
インプットだから、1周目よりも復習こそ大事です。
英単語帳を一周しかしない人はいないでしょう。
使う教材は流石に古いですが、青チャートの例題というのは今でも悪くありません。
今なら東京出版の1対1対応の演習でしょう。
私の
という記事も、暗記数学の系譜を受け継いでいます。
（そして、さらに極端にインプットに傾けています。）
暗記数学の招く誤解
ここまでは、良いのです。
暗記数学はそのネーミングから、様々な誤解を生みます。
数学の教師で誤解している人は多くないと信じていますが、受験生や、エセ講師は間違った解釈をしている人がとても多いです。
和田秀樹さんは「理解しなくて良い。暗記しろ。」ということを言います。だから暗記数学です。
ですが、これを文字通り真に受けるのは本当に危険です。
和田秀樹さん自身も、本当に全く理解せずに暗記していたわけではありません。
エビングハンスの忘却曲線というものがあります。
これを持ち出して、覚えたことの8割は明日には忘れているという人がいます。
が、これは意味のないスペルを覚えさせられた実験です。
人間は意味を関連付けると記憶が強固になります。
数学の解法は理解すれば自然に覚えられる程度の分量なのです。
逆に理解しないとかなり覚えにくいと思います。
理解なしに解答を最初から最後まで覚えようとするとどうなるでしょう。
例えばベクトルの基礎から標準レベルの有名問題にこういうのがあります。
この手描き感は6/13に発売したiPad Proで描きました。ふふふ。
解答はこんな感じです。
どうでしょうか。これをお経のように唱えて覚えるんですか？
絶対に受かりませんね笑
和田秀樹さんもこのようにはやっていないはずです。
解答を理解すると、解けるようになる確率が大幅にアップします。
実はこの問題で覚えることはただ一つ
「ベクトルの問題は始点を揃えると上手くいくかも」
これだけです。これさえ頭に入れておけば、あとは自然に解けるはずです。
解けない？それなら黄チャートをやりましょう。
暗記数学とは「ベクトルの問題は始点を揃えると上手くいくかも」を理由を深追いせずに覚えることです。
そこから先は解答を理解できたら再現できます。
ちなみに、もう少し上の段階に進めばベクトルの始点を揃えるのは当たり前に思えます。
だって、慣れ親しんだ平面座標だって2本のベクトルです。空間座標は3本のベクトルです。
これの始点がバラバラだったら、ある点を表すのが大変なのは想像できますね。
平面図形の問題だから、上手くいけば、始点の同じ2本のベクトルだけで、全部表せるはずですね。
それがたまたま垂直に交わってるのが平面座標であって、斜めでもいいんです。こんな感じで。
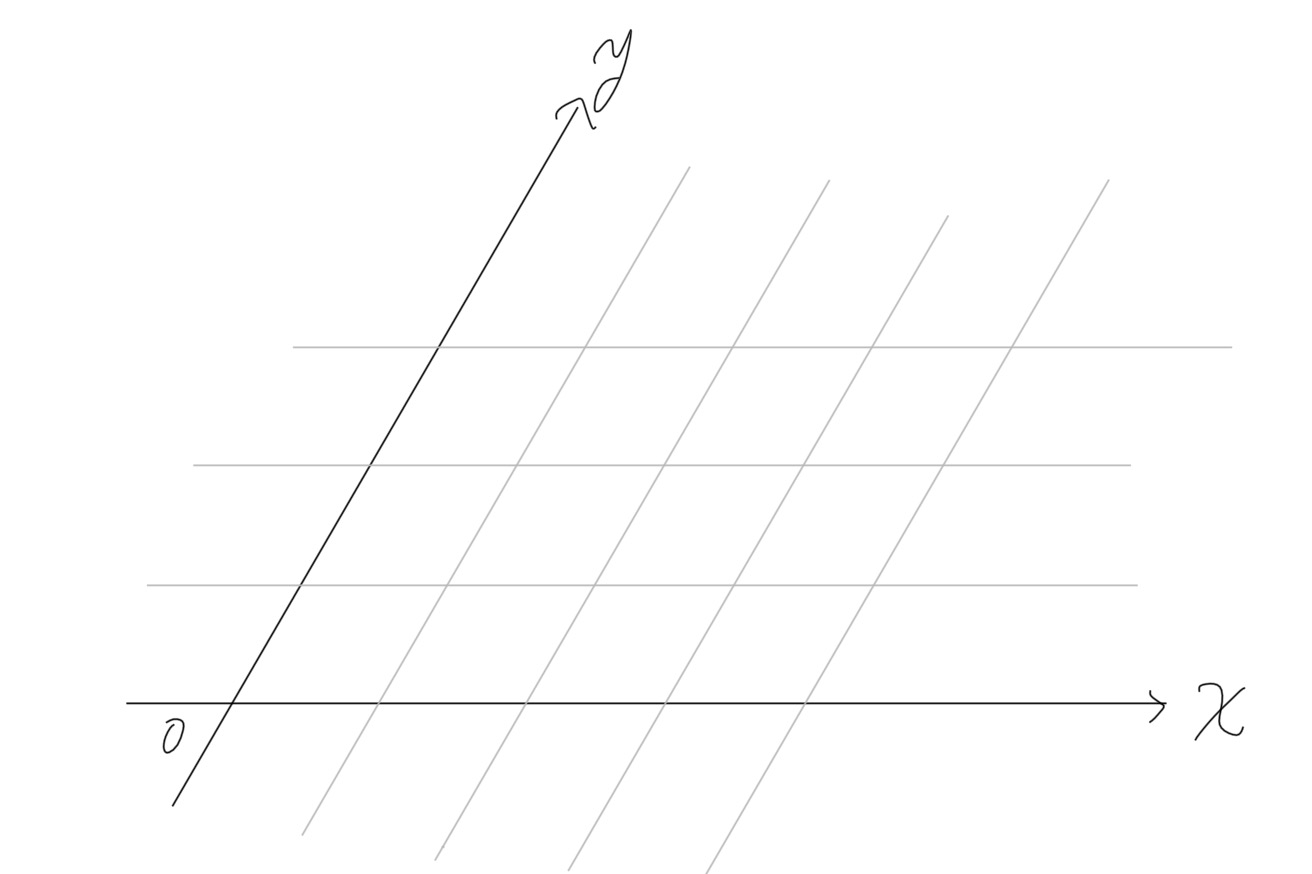だから、なんかたくさんベクトルが出てきても、始点さえ揃えれば2種類にまとまる（はず）です。
まあ条件によってはまとまらないでしょう。
でも、そんな直感的な理解が得られれば、なお頭に残りますね。
ちなみに、私は数学でも他の教科でも、直感的な理解を大事にするべきだと思います。
厳密さを追い求めると、
２点を結ぶ最短距離が直線だとしたら、なぜそれは１本なんだろう…
みたいな恐ろしい深淵を覗くことになります。
この問いが恐ろしいという勘が働くとセンスがあります。
勉強と理解の関係については
という記事を読んで下さい。
以上、暗記数学とは一体なんなのかでした。
コメントを残す