大学受験で一番惜しい失点は計算ミスだと思います。

理系科目の場合、解き方を覚えるとか、思いつくとか、そういう能力に目が行きますが、

速くて安定した計算力が大前提として必要です。

大学受験生なら優先度はかなり高いでしょう。

毎日トレーニングをするべきです。

ですが、今回は試験本番で使える、計算ミスを減らす方法（文字計算編）を書きます。

計算についての基礎知識

まずは数値計算と文字計算があることを知りましょう。

数値計算力と文字計算力は結構違います。片方は速いけれど片方は遅い人がたくさんいます。

文字計算であれば1式で1文字消せます。

なので、4文字3式（消さなくていい、答えに書いていい文字はカウントしない）になったら立式で間違っている可能性が高いです。

単位に注目する

これは文字計算で発揮される技術です。

立式の時点で、または答えの時点で単位があってるか確認します。

これは物理や化学で単位の概念をある程度知っていないといけませんね。

物理で力Fを求めよと言われて

計算結果が\(4\sqrt {mg}\)

になった瞬間に間違ってることに気づかなければなりません。

なぜなら、単位が合わないから。

力の単位はニュートン[N]ですが、F=maなので[kg･m/s²]でもありますね。

\(4\sqrt {mg}\)はルートの中にmaと同じ単位のものが入ってるので絶対に合いませんね。

単位については奥が深すぎるので今後別の記事を書くことにします。

何か代入してみる

これは凄く初歩なものから高度なものまであります。

初級編

$$\sum ^{n}_{k=1}k^{2}=\frac {1}{6}n\left( n+1\right) \left( 2n+1\right)$$ 

みたいなのにn=1とか2とか3を入れてみて辻褄が合うかやってみるということです。

話は逸れますが上の式の導出はできますか？

これの導出はシグマの計算の基本が詰まっていますよ。

つまり

$$\sum ^{n}_{k=1}\left( ak^{2}+k\right) =a\sum ^{n}_{k=1}k^{2}+\sum ^{n}_{k=1}k$$

みたいなやつですね。

ちなみに私は大学受験を終えて長い年月を経てこういう公式は何度も忘れかけていますが、導けるのでこうして記事が書けるのです。

ちなみにこうやります

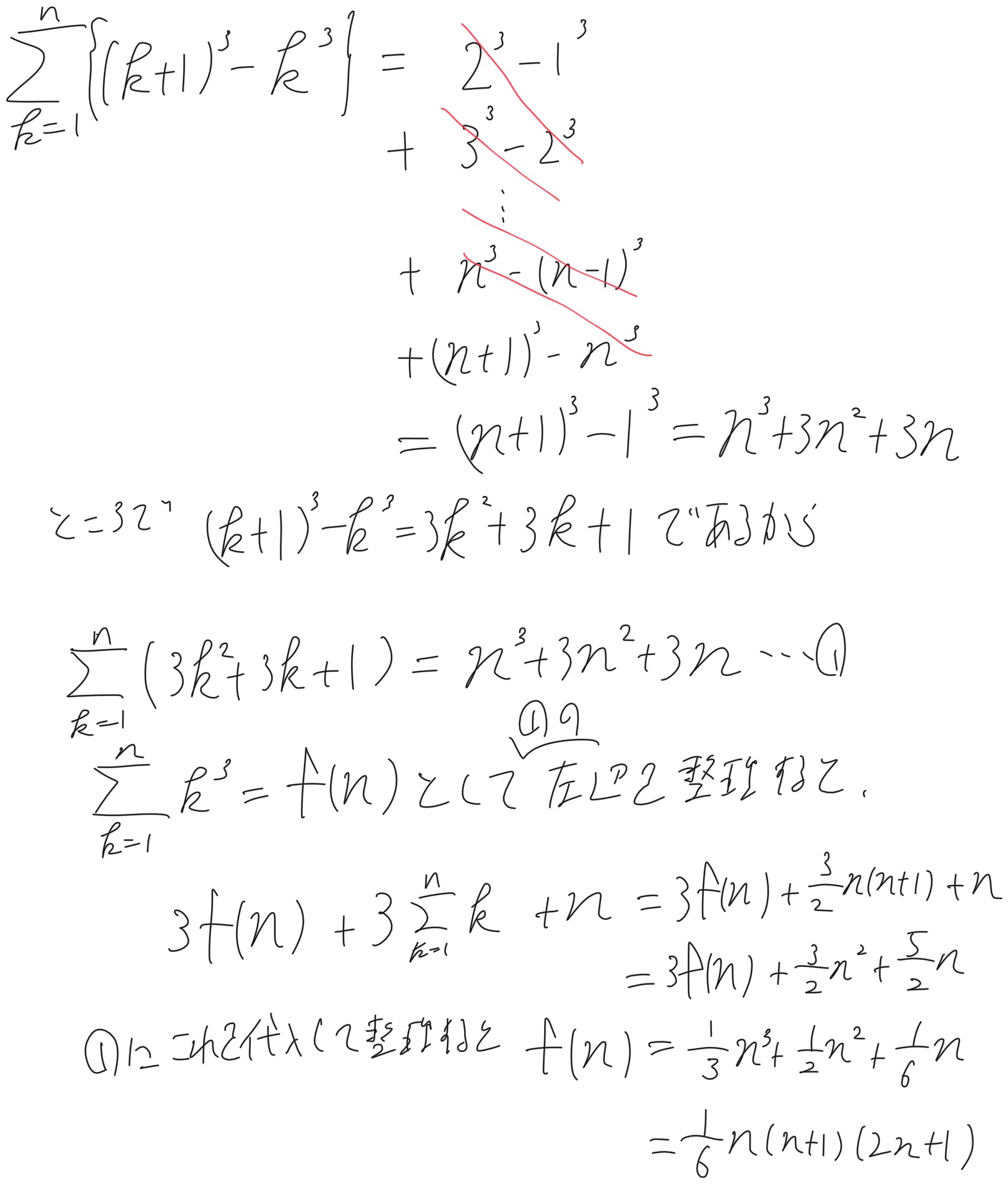
は？1行目どっから降ってきたんだよ？と感じるのはごもっともですが、これが数列の発想法なのです。

ちなみに等比数列の和の公式もなんとなく似た感じで導出しますし、等比数列の和の公式の導出ができると等比×等差みたいな応用問題も解けます。

なんて、話が逸れました。

まあともかくn=1とか2とか代入して辻褄が合うかやってみるのが計算チェックの初級です。

もうちょっと難しくなるとどうでしょうか。

上級編

例えを物理にしてみますか

斜面の角度を段々きつくしていき、角度θになったところでちょうど滑り出した。

静止摩擦係数μを求めよ。という問題だとします。

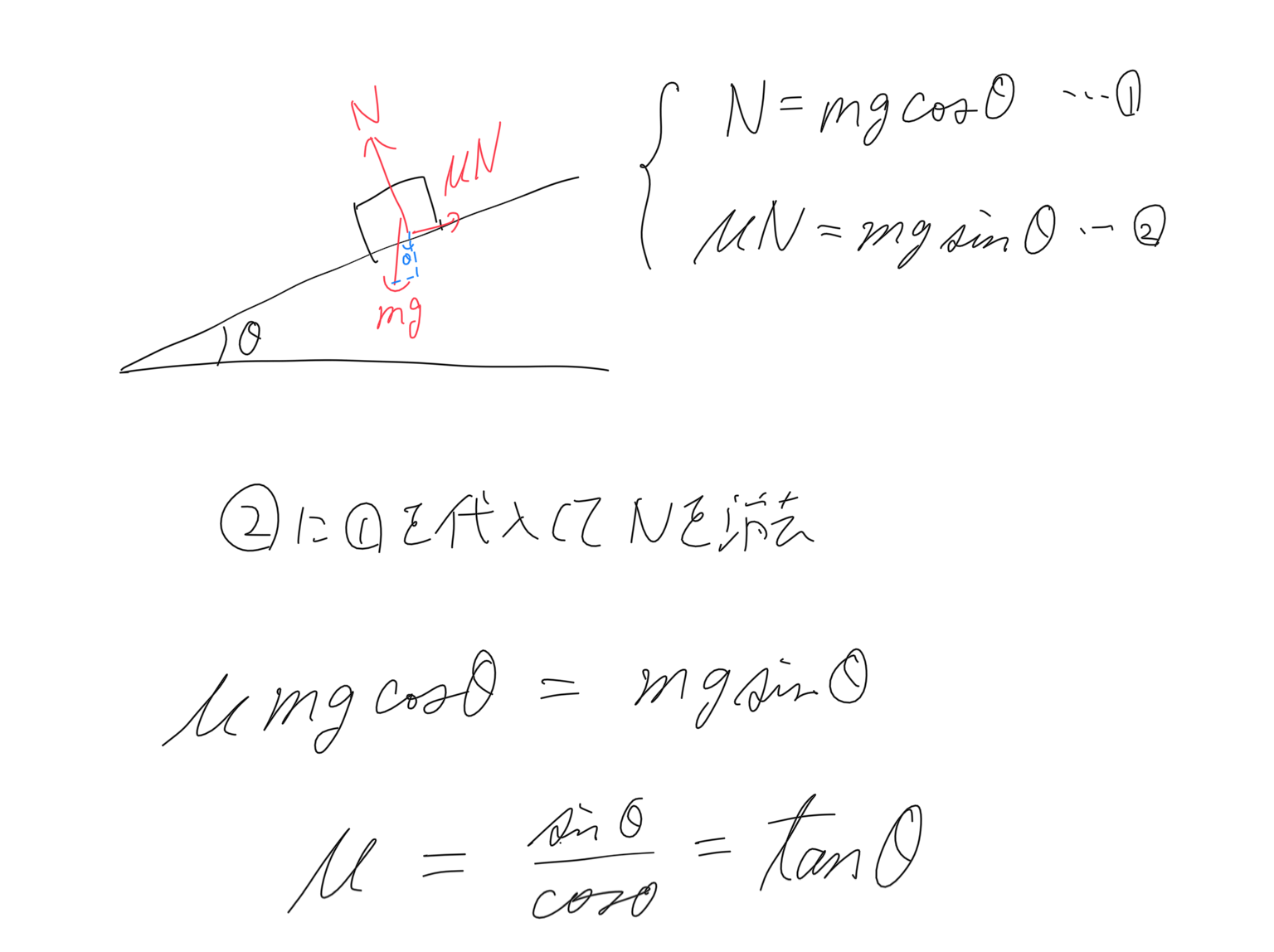さてさて、この問題そのものにもツッコミどころは満載で

問題文を読むとθしか与えられていませんから、mとかgとかNとか勝手に置いてますね。

でも答えにこれらの文字を使ったら問題文に答えてないんですね。まあ、問題に不備がなければですが。勉強が進んで問題に不備があることが分かれば作問者への嫌味として（重力加速度をgとする）なんて断って答えに入れたりしますね。

ところがこの問題に不備はないのです。

それから、「立式の時点でmとgとNを消さないといけないのに2式しかない…終わった」と思った方はセンスが良いです。

3文字消すなら3式必要という原則が分かってるんですね。

3文字消すのに3式使ってしまうと今度はμが求まらないので、4式必要ということになりますが…

なんとNとmとgは今回は実は全部合わせて1文字なんですね。

だってX=mg/NとおけばXだけで表されてしまいますからね。

またまた横道にそれました。すみません。

さてこの問題は良問で、答えはμ=tanθなのですが、計算チェックが2通りで出来るのです。

今回の代入してみるですね。

1とか2とか代入するわけにはいかないので、どうするかというと極端な値を入れてみるんですね。

θ=0とすると、μも0になりますね。

確かに静止摩擦係数が0に近ければ、ほぼ0度で動き出すわけですからあってそうですね。

θ=90°に近いものを入れるとμは無限大に近くなりますね。これも直感的にわかります。

こんな感じです。

このチェックをする習慣があれば計算を間違えてcosθという答えになったら間違いに気づけます。

もう一つ上で書いたチェックが使えます。

単位ですね。

静止摩擦係数の単位はなんでしょう？

単位なしが答えです。係数ですからね。

tanθにも単位はありませんから合ってそうですね。

最後に超上級編…

極端な値を入れるというのは直感的に合ってるかというセンス、どんな値をいれるべきかというセンスが問われます。

上で書いたのはまだ易しいのですよ。

もっとむごい難問でも活躍します。

と思ったら最新の慶應医学部の過去問がちょっと簡単だったので言うほど超上級ではないのですが…

これの(1)の答えが

$$p_{n}=\frac {3}{4}+\frac {1}{4}\left( -\frac {1}{3}\right) ^{n}$$

になるのですが、状況が分かるでしょうか。

これは確率漸化式という、なぜか慶應医学部で毎年出題される問題です。

派手な問題ですが、ハイレベルな受験生にとってはスタンダードな確率のほうが怖いでしょうね。派手ですが、確率漸化式はワンパターンです。

というわけで慶應医学部を受験する人は絶対に得点源にしましょう。

さて、これはAという状況とBという状況を一定の確率で行ったり来たりするのですが、

そういう目で見ると(1)の答えの数式の意味が分かってきます。

要するに平衡状態と偶奇の関係が見えてきます。

この問題では「Aからスタートして1/3の確率でBに移行する。2/3の確率でAに留まる。逆にBからは絶対にAに移行する」ということですから

1回目でAにいる確率は2/3

2回目はAAかBAだから4/9+1/3=7/9

3回目はAAA、ABA、BAA、の3通りで8/27+2/9+2/9=20/27

つまり上がったり下がったりしてますね。偶数回は若干Aにいる確率が高いのですね。

それが上の答えに反映されているでしょう。

それからもう一つ、化学平衡のように考えることも出来ます。

上がったり下がったりするものの、直感的にかなりの数をこなせば今何回目か関係なくなってくるはずです。

だってAとBを一定の確率で行き来するだけですから、確率は収束するはずです。

してますね。これもOK。

最後にもう一つ、収束するということは平衡が成り立ってるはずです。

Aの1/3がBに移行して、BのすべてがAに移行するのに平衡なのです。

だからA:Bが3:1つまり、答えが3/4に収束するはずなのです。

してますね。

これで計算ミスしている確率は低いといえます。

終わりに

計算力というと力技のイメージです。

実際、力技は馬鹿にしてはいけない、というより鍛えれば鍛えるほど合格に近づきます。

ですが、こういう技巧的というか、理系的な思考力で成り立つ部分も大いにあるのです。

特に超上級編は結構センスが問われますね。

最後は数3的な考察ですし、物理の分野からも多く例を挙げてしまいました。

まあ最後の方は理解できなくても普通です。

お気になさらず。

以上、計算ミスを減らす方法でした。