理解するとはなにか

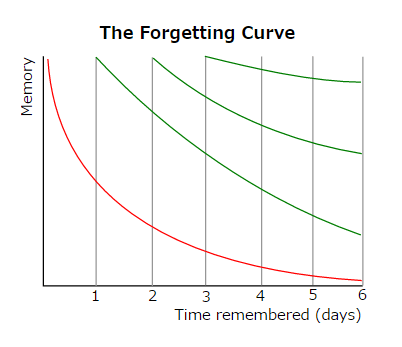
エビングハウスの忘却曲線という言葉を聞いたことがあるでしょうか。

私がリリースしているSuper Flash Cardというアプリは

エビングハウスの忘却曲線に基いて復習のタイミングを自動で管理するのが売りです。

ここでポイントなのが

エビングハウスの忘却曲線は意味のない文字列を覚えた場合の忘却する様子をグラフにしていることです。

理解すると忘却は起こりにくくなることが知られています。

では理解するとは何か。

公式を導出できること？

そうとは限りません。

日本史の勉強でも「○○という時代背景があって民衆の不満が…」と理解すると記憶しやすくなります。

まあそれ自体が出題されたりするんですが。

理解する方法は2つあります。

1 つは、日本史の例で挙げた「なるほど納得」式 の「ごく自然であると感じる」ようにする方法です。

「腑に落ちる」という表現が言い得て妙と思います。

もう 1 つは、感覚的には完全 には納得していないけれども、正しいことから出発し

そして「論理」によっ て「それ以外にはあり得ない」との結論を得る方法です。

難しく言うとデカルトの演繹ですね。

高校数学では後者の割合が高くなりますが、

得意な人ほど実は腑に落ちています。

割り箸でやってみれば「3辺相当で合同」も腑に落ちます。

3つの割り箸の長さを決めてやると同じ形の三角形しか作れないですから。

同様に「二辺夾角相当で合同」とかも理解できると思います。

数学以外の科目に関しては、より腑に落ちる理解が大切です。

勉強の際、いかに自分の腑に落とせるかが腕の見せどころです。

ただし英単語や古文単語のような単純な暗記では腑に落とすより単純に暗記するほうが早いでしょう。

ちなみに「predictはpre＋dictだ。preは前、dictはdictationやdictionaryと同じで言うという意味があるのだ。だから予言になるのだ。」

という説明もあったりしますが、全ての単語に面白いわかりやすい語源があるわけではありません。

普通に暗記するほうが早いです。

その際はSuper Flash Cardをご利用下さい。

以上、理解するとは何か、でした。